Data Structures in C++

At Programming Homework Tutors, we believe in providing our students with practical, real-world examples of how to apply the concepts they learn in class. That’s why we’ve developed a variety of sample projects to help you see how our courses can be used to create impactful solutions in your field of study.

Please typeset your answers to the following homework problems (you may save this file as week8hwk_your_lastname.doc and then directly type your answers after each problem). Submit this assignment on Blackboard after you have finished by the due time.

The Fibonacci sequence is the series of integers

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

See the pattern? Each element in the series is the sum of the preceding two items. There is a recursive formula for calculating the n-th number of the sequence (the 0-th number if Fibonacci(0)=0):

Fibonacci(n) = n, if n = 0 or 1, and

Fibonacci(n) = Fibonacci(n-2) + Fibonacci(n-1), if n > 1

Write a recursive version of the C++ function Fibonacci.

Every budding computer scientist must grapple with certain classic problems. The tower of Hanoi (see the Figure below) is one of the most famous of these. Legend has it that in a temple in the Far East, priests are attempting to move a stack of disks from on peg to another. The initial stack had 64 disks threaded onto one peg and arranged from bottom to top by decreasing size. The priests are attempting to move the stack from this peg to a second peg under the constraints that exactly one disk is moved at a time, and at no time may a larger disk be placed above a smaller disk. A third peg is available for temporarily holding disks. Supposedly, the world will end when the priests complete their tasks, so there is little incentive for us to facilitate their efforts.

Figure: The Tower of Hanoi for the case with three disks.

Let us assume that the priests are attempting to move the disks from peg 1 to peg 3. We wish to develop an algorithm that will print the precise sequence of peg-to-peg disk transfers.

If we were to approach this problem with conventional methods, we would rapidly find ourselves hopelessly knotted up in managing the disks. Instead, if we attack the problem with recursion in mind, it immediately becomes tractable. Moving n disks can be viewed in terms of moving only n-1 disks (hence, the recursion), as follows:

Move n-1 disks from peg 1 to peg 2, using peg 3 as a temporary holding area.

Move the last disk (the largest) from peg 1 to peg 3.

Move the n-1 disks from peg 2 to peg 3, using peg 1 as a temporary holding area.

The process ends when the last task involves moving n=1 disk, i.e., the base case. This is accomplished by trivially moving the disk without the need for a temporary holding area.

Write a program to solve the Towers of Hanoi problem and show your testing results for the case of moving a stack of five disks from peg 1 to peg 3. Use a recursive function (i.e., the function calls itself in the function body) with four parameters:

(a)  The number of disks to be moved.

       (b)  The peg on which these disks are initially threaded.

       (c)  The peg on which this stack of disks is to be moved.

       (d)  The peg to be used as a temporary holding area.

Your program should print the precise instructions it will take to move the disks from the starting peg to the destination peg. For example, to move a stack of three disks from peg 1 to peg 3, your program should print the following series of moves;

       1 –> 3 (This means move one disk from peg 1 to peg 3)

1 –> 2

3 –> 2

1 –> 3

2 –> 1

2 –> 3

1 –> 3

Mark the following statements as true or false.

A binary tree must be nonempty.

The level of the root node is 0.

If a tree has only one node, the height of this tree is 0 because the number of levels is 0.

The inorder traversal of a binary tree always outputs the data in ascending order.

Problems 4-9 will be using the following binary tree.

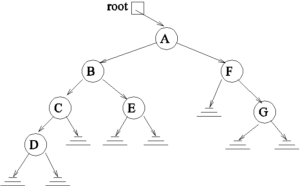
Find L_A, the node in the left subtree of A.

Find R_A, the node in the right subtree of A.

Find R_B, the node in the left subtree of B.

List the nodes of this binary tree in an inorder sequence.

List the nodes of this binary tree in a preorder sequence.

List the nodes of this binary tree in a postorder sequence.

Problems 10-14 will be using the following binary search tree.

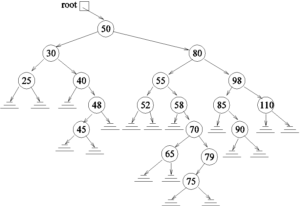
List the path from the node with info 80 to the node with info 79.

A node with info 35 is to be inserted in the tree. List the nodes that are visited by the function insert to insert 35. Redraw the tree after inserting 35. (You may draw on a paper and then scan it or take a picture of it and insert the picture in your solutions file.)

Delete the node 52 and redraw the binary tree. (You may draw on a paper and then scan it or take a picture of it and insert the picture in your solutions file.)

Delete the node 40 and redraw the binary tree. (You may draw on a paper and then scan it or take a picture of it and insert the picture in your solutions file.)

Delete nodes 80 and 58 in that order. Redraw the binary tree after each deletion. (You may draw on a paper and then scan it or take a picture of it and insert the picture in your solutions file.)

Disclaimer

The sample projects provided on our website are intended to be used as a guide and reference for educational purposes only. While we have made every effort to ensure that the projects are accurate and up-to-date, we do not guarantee their accuracy or completeness. The projects should be used at your own discretion, and we are not responsible for any loss or damage that may result from their use.
At Programming Homework Tutors, we are dedicated to helping students and educators achieve their goals by providing them with the resources they need to succeed. Our website offers a variety of tools and resources that can help you with the project mentioned above.
Whether you need help with research, project management, or technical support, our team of experts is here to assist you every step of the way. We offer online courses, tutorials, and community forums where you can connect with other learners and get the support you need to succeed.
If you’re looking to take your skills to the next level and make an impact in your field, we invite you to explore our website and see how we can help you achieve your goals.